Referat

Thema: Der logische Fehler im Gottesbeweis des Thomas von Aquin

Referent: Johannes Wienand

Dozent: Clemens Weidmann

Sommersemester 2001

Universität Wien

Der dritte Gottesbeweis des Thomas von Aquin.
(lateinisches Original)

Tertia via est sumpta ex possibili et necessario: quae talis est.
Invenimus enim in rebus quaedam quae sunt possibilia esse et non esse: cum quaedam inveniantur generari et corrumpi, et per consequens possibilia esse et non esse. Impossibile est autem omnia quae sunt talia [semper] esse: quia quod possibile est non esse, quandoque non est. Si igitur omnia sunt possibilia non esse, aliquando nihil fuit in rebus. Sed si hoc est verum, etiam nunc nihil esset: quia quod non est, non incipit esse nisi per aliquid inciperet esse, et sicmodo nihil esset: quod patet esse falsum. Non ergo omnia entia sunt possibilia: sed oportet aliquid esse necessarium in rebus.
Omne autem necessarium vel habet causam suae necessitatis aliunde, vel non habet. Non est autem possibile quod procedatur in infinitum sicut nec in causis efficientibus, ut probatum est. Ergo necesse est ponere aliquid quod sit per se necessarium, non habens causam necessitatis aliunde, sed quod est causa necessitatis aliis:
quod omnes dicunt Deum.

Der dritte Gottesbeweis des Thomas von Aquin
(deutsche Übersetzung)
Der dritte Weg zur Erkenntnis Gottes geht von den Begriffen des Möglichen und des Notwendigen aus und verläuft wie folgt:
(a)
 Wir finden unter den Dingen nämlich solche, deren Existenz wie deren Nichtexistenz gleichermaßen möglich ist, da sie irgendwann entstehen und wieder vergehen. Für alle diese Dinge ist es unmöglich, ewig zu existieren, weil etwas, dessen Nicht-Existenz möglich ist, auch zu irgendeiner Zeit nicht existiert. Wenn aber für schlechthin alles zutreffen sollte, dass seine Nicht-Existenz möglich ist, dann muss es auch eine Zeit gegeben haben, in der tatsächlich nichts existierte. Wenn das aber der Fall wäre, dann würde auch heute nichts existieren; denn etwas, das nicht existiert, beginnt nur durch etwas anderes zu existieren, das seinerseits schon existiert. Wenn also irgendwann einmal nichts existierte, dann konnte auch nichts zu existieren beginnen, und es würde zu keiner Zeit etwas existieren. Dies ist aber offensichtlich falsch. Deshalb sind nicht alle Dinge in ihrer Existenz nur möglich; es muss irgend etwas geben, dessen Existenz notwendig ist.
(b) Jedes Notwendige hat aber die Ursache seiner Notwendigkeit entweder von anderswoher oder nicht. Es ist aber nicht möglich, dass es ins Unendliche bei den notwendigen Dingen gehe, die eine Ursache ihrer Notwendigkeit haben, wie dies auch bei den Wirkursachen nicht möglich ist, wie oben bewiesen.
(c) Also ist es notwendig etwas anzunehmen, das an sich notwendig ist und die Ursache seiner Notwendigkeit nicht von anderswoher hat, sondern das vielmehr Ursache der Notwendigkeit für die anderen Dinge ist.
Dies nennen alle Gott.

Thomas Aquinus

Thomas von Aquin, der bedeutendste Theologe und Philosoph des Mittelalters, wurde um 1225 in Roccasecca bei Aquino geboren. Er fasste den überlieferten Augustinismus mit den Lehren des Aristoteles, die damals erst in ihrem ganzen Umfang im Abendland bekannt wurden, in einer philosophisch-theologischen Synthese zusammen. Über Augustinus und andere wirkten auch platonische und neuplatonische Gedanken auf ihn ein. - Thomas von Aquin erkannte die Berechtigung des Wissens neben dem Glauben und die Bedeutung einer eigenständigen Philosophie an. Da das Wissen zu seiner Vollendung des Glaubens bedarf, ordnete er die Philosophie der Theologie unter. - Die Einheit seines Systems ist darin begründet, dass alle Einzelsätze auf wenige ontologische Grundprinzipien zurückgeführt weren. Alles innerweltlich Seiende galt ihm als 'durch Teilhabe seiend' und darum verursacht. So steigt Thomas von Aquin in seinen fünf Gottesbeweisen vom Irdischen zu Gott als der 'ersten Ursache' auf. Voraussetzung dieser natürlichen Gotteserkenntnis ist die 'Analogie des Seienden', d.h. eine gewisse, trotz aller Unähnlichkeit bleibende Ähnlichkeit des Geschöpfes mit Gott. Freilich bleibt die natürliche Gotteserkenntnsis ohne letzte Sicherheit; nur durch göttliche Offenbarung vermöge die meschliche Vernunft mehr über Gott zu sagen. Thomas von Aquin starb 1274 auf der Reise zum Konzil von Lyon im Kloster Fossanuova.

Die aristotelische Logik

Die formale Logik ist als eigenständige Wissenschaft von Aristoteles begründet worden. Er stellte seine Logik - die Bezeichnung taucht erstmals bei ALexander von Aphrodisias auf - als 'Werkzeug' sämtlichen anderen Disziplinen voran (logische Propädeutik). Besonders seine ausgearbeitet Theorie des Syllogismus (als Vorläufer eines Teils der heutigen Prädikatenlogik) bestimmte die Geschichte der Logik für fast zwei Jahrtausende.
Die Logik untersucht die Strukur von so genannten Aussagen (Sätzen), die entweder wahr oder falsch sein können. Ein Argument, eine Verknüpfung mehrerer Aussagen, besteht aus den Annahmen (Prämissen) und der Schlussfolgerung (Konklusion).
 
Beispiel für ein gültiges Argument mit zwei Prämissen:
 
Alle Menschen sind sterblich.  Erste Prämisse
Aristoteles ist ein Mensch.  Zweite Prämisse
Also ist Aristoteles sterblich.  Konklusion

Formalisierung der natürlichen Sprache

Die formale Logik versucht nun ein System zu entwickeln, in dem Sätze völlig ohne die in einer natürlichen Sprache üblichen Ungenauigkeiten ausgesagt werden können. Dazu wird eine stark formalisierte eigene Sprache entwickelt: die logische Sprache. Ein Satz der natürlichen Sprache wird nun in seine Bestandteile zerlegt und analysiert. Subjekte werden durch Individuenkonstanten (a, b, c, ...) oder Individuenvariablen ersetzt (x, y, z, ...), Prädikate durch Prädikatbuchstaben (A, B, C, ...).
Das obige Beispiel könnte nun wie folgt formuliert werden:
 
Beispiel für ein gültiges Argument mit zwei Prämissen:
 
1. Für alle x gilt, wenn x die Eigenschaft M hat (nämlich die Eigenschaft, ein Mensch zu sein), dann hat x ebenfalls die Eigenschaft S (nämlich die Eigenschaft, sterblich zu sein).  Erste Prämisse
2. Es gibt mindestens ein a. Dieses a hat die Eigenschaft A (nämlich Aristoteles zu heißen) und dieses a hat ebenfalls die Eigenschaft M (nämlich ein Mensch zu sein).  Zweite Prämisse
3. Also: Es gibt mindestens ein a. Dieses a hat die Eigenschaft A (nämlich Aristoteles zu heißen) und dieses a hat ebenfalls die Eigenschaft S (nämlich sterblich zu sein).  Konklusion

 
Dieses Argument kann wie folgt vereinfacht werden:
 
1. Für alle x gilt: wenn Mx dann Sx.  Erste Prämisse
2. Es gibt mindestens ein a für das gilt: Aa und Ma.  Zweite Prämisse
3. Also: Es gibt mindestens ein a für das gilt: Aa und Sa.  Konklusion

Diese formalisierte Fassung des Satzes lässt die grammatische Struktur der Aussage wesentlich deutlicher erkennen, als die umgangssprachliche Formulierung. Die Aussagen können aber noch weiter analysiert werden, indem man die Bedeutung der oben unterstrichen dargestellten Satzteile analysiert.

Logische Verknüpfungen

Ein Satz der natürlichen Sprache besteht außer aus Individuenvariablen, Individuenkonstanten und Prädikatbuchstaben zusätzlich noch aus logischen Verknüfungen der einzelnen Satzteile, aus den so genannten Konnektiven. Solche Verknüfungen sind etwa das "wenn ... dann ..." oder das "... und ...", mit denen zwei Satzbestandteile zu einem neuen, komplexeren Satz zusammengesetzt werden können. In der formalen Logik gibt es für solche Konnektive eigene Zeichen:
 
Symbol Fachausdruck Umgangssprache
Konjunktion "und"
Konditional "wenn ... dann"
Universalquantifikator "für alle x gilt: ..."
Existenzialquantifikator "es gibt mindestens ein x für das gilt: ..."

 
Das obige Beispiel lässt sich nun also wie folgt aufschreiben:
 
1.  Erste Prämisse
2.  Zweite Prämisse
3.  Konklusion

Weiter kann der Satz nun nicht mehr vereinfacht, bzw. formalisiert werden.

Sportwagen und Millionäre

Um den logischen Fehler im dritten Gottesbeweis des Thomas von Aquin als einen solchen zu entdecken, benötigt man nun keine weiteren Kenntnisse der formalen klassischen Logik. Dennoch sind einige Vorüberlegungen und ein Minimum an Mengenlehre nötig, um den Fehler richtig zu interpretieren. Doch zunächst bleiben wir noch bei Sätzen der natürlichen Sprache.

Schauen wir uns folgendes Beispiel an:
1. Jeder Millionär besitzt (mindestens) einen Sportwagen.

Dieser Satz sagt folgendes aus:
(a) Es gibt eine Menge von Millionären. Diese Menge ist nicht leer, das heißt, sie enthält mindestens ein Element, nämlich mindestens einen Millionär.
(b) Es gibt eine Menge von Sportwagen. Auch diese Menge ist nicht leer, das heißt, sie enthält mindestens ein Element, in diesem Fall mindestens einen Sportwagen.
(c) Jedes Element der Menge M (also jeder Millionär), steht in einer bestimmten Relation (nämlich in einem Besitzverhältnis) zu einem Element der Menge S (also zu einem Sportwagen).
Der Satz besagt, dass die verschiedenen Millionäre durchaus auch verschiedene Sportwagen besitzen können. Es ist lediglich vorgegeben, dass jeder Millionär (mindestens) einen Sportwagen besitzt - welchen ist dabei völlig egal.
Schauen wir uns einen zweiten Satz an, den man auf den ersten Blick als die Umkehrung des Satzes 1 betrachten könnte:
2. Es gibt (mindestens) einen Sportwagen, den jeder Millionär besitzt.

Dieser Satz besagt im Gegensatz zu Satz 1, dass jeder Millionär (mindestens) ein und den selben Sportwagen besitzt (mindestens bedeutet hier, dass er darüber hinaus noch andere Sportwagen besitzen kann, dass aber mindestens dieser eine bestimmte Sportwagen darunter sein muss). Dieser kleine, aber feine Unterschied ist in der deutschen Sprache nicht auf Anhieb erkennbar. Formalisiert man jedoch die beiden Sätze mithilfe der formalen Logik, wird schnell deutlich, dass es sich bei den beiden Sätzen um zwei grundverschiedene Bedeutungen handelt:
1. 
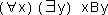2. 
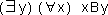Zeichenerklärung:
x ist ein Element der Menge der Millionäre
y ist ein Element der Menge der Sportwagen
B ist die Relation zwischen x und y, in diesem Fall das Besitzverhältnis.

Aussage 1 besagt, dass jeder Millionär den einen oder anderen Sportwagen besitzt. Es kann also der eine einen Porsche fahren, der andere einen Ferrari etc. Wichtig ist nur, dass jeder Millionär irgendeinen Sportwagen sein eigen nennen kann.
Die Aussage 2 hingegen behauptet, dass es einen ganz bestimmten Sportwagen gibt (zum Beispiel einen Ferrari), den alle Millionäre besitzen. Jeder Millionär hätte somit also einen Ferrari in der Garage stehen.

Der logische Fehler bei Thomas von Aquin

Der Fehler, den Thomas von Aquin in seinem dritten Gottesbeweis macht, ist von der selben Art wie der obige Fehler mit den Sportwagen und den Millionären. Die fragliche Textstelle ist folgende:
1. Für alle diese Dinge ist es unmöglich, ewig zu existieren, weil etwas, dessen Nicht-Existenz möglich ist, auch zu irgendeiner Zeit nicht existiert.
2. Wenn aber für schlechthin alles zutreffen sollte, dass seine Nicht-Existenz möglich ist, dann muss es auch eine Zeit gegeben haben, in der tatsächlich nichts existierte.
Um den Fehlschluss zu verdeutlichen, muss diese Textstelle wieder genau analysiert und formalisiert werden. Auf diese Art und Weise erhält man folgende Sätze:
 
1.  Für jedes Ding gibt es (mindestens) einen Zeitpunkt, zu dem es nicht existiert.
2.  Es gibt (mindestens) einen Zeitpunkt, zu dem jedes Ding nicht existiert.
Satz 2. lässt sich wie folgt umschreiben:
2a)  Es gibt (mindestens) einen Zeitpunkt, zu dem kein Ding existiert.

Formalisiert sieht das Argument dann wie folgt aus:
 
1.
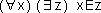2.
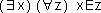Zeichenerklärung:
x ist ein Element der Menge der Dinge (also ein Ding)
z ist ein Element der Menge der Zeitpunkte (also ein Zeitpunkt)
E ist die Relation zwischen x und z und besagt in diesem Fall, dass x zum Zeitpunkt z nicht existiert.

Jetzt wird deutlich, dass Thomas von Aquin eine in der Logik unzulässige Umformung vorgenommen hat. Die Wahrheit einer Aussage darf verständlicherweise unter einer formalen Transformation nicht leiden. Doch eben dies tut sie hier. Während im Satz 1 jedem Ding mindestens ein bestimmter Zeitpunkt zukommt, an dem es nicht existiert - es können ohne weiteres für jedes Ding verschiedene Zeitpunkte sein - gibt es im Satz 2 mindestens einen bestimmten Zeitpunkt, an dem kein einziges Ding existiert.
Wie somit gezeigt werden konnte, ist der dritte Gottesbeweis des Thomas von Aquin formallogisch ungültig.
--> [ jo ]